riemann hypothesis

Riemann Hypothesis

A more general statement known as the generalized Riemann hypothesis conjectures that neither the Riemann zeta function nor any Dirichlet L-series has a zero with real part larger than 1/2.

Legend holds that the copy of Riemann's collected works found in Hurwitz's library after his death would automatically fall open to the page on which the Riemann hypothesis was stated (Edwards 2001, p. ix).

Proof of the Riemann hypothesis is number 8 of Hilbert's problems and number 1 of Smale's problems .

In 2000, the Clay Mathematics Institute ( http://www.claymath.org/ ) offered a $1 million prize ( http://www.claymath.org/millennium/Rules_etc/ ) for proof of the Riemann hypothesis. Interestingly, disproof of the Riemann hypothesis (e.g., by using a computer to actually find a zero off the critical line ), does not earn the $1 million award.

	source
	Brent et al. (1982)
	Wedeniwski/ZetaGrid
	Gourdon (2004)

The Riemann hypothesis is equivalent to the statement that all the zeros of the Dirichlet eta function (a.k.a. the alternating zeta function)

By modifying a criterion of Robin (1984), Lagarias (2000) showed that the Riemann hypothesis is equivalent to the statement that

There is also a finite analog of the Riemann hypothesis concerning the location of zeros for function fields defined by equations such as

According to Fields medalist Enrico Bombieri, "The failure of the Riemann hypothesis would create havoc in the distribution of prime numbers" (Havil 2003, p. 205).

In Ron Howard's 2001 film A Beautiful Mind , John Nash (played by Russell Crowe) is hindered in his attempts to solve the Riemann hypothesis by the medication he is taking to treat his schizophrenia.

In the Season 1 episode " Prime Suspect " (2005) of the television crime drama NUMB3RS , math genius Charlie Eppes realizes that character Ethan's daughter has been kidnapped because he is close to solving the Riemann hypothesis, which allegedly would allow the perpetrators to break essentially all internet security.

In the novel Life After Genius (Jacoby 2008), the main character Theodore "Mead" Fegley (who is only 18 and a college senior) tries to prove the Riemann Hypothesis for his senior year research project. He also uses a Cray Supercomputer to calculate several billion zeroes of the Riemann zeta function. In several dream sequences within the book, Mead has conversations with Bernhard Riemann about the problem and mathematics in general.

Portions of this entry contributed by Len Goodman

Explore with Wolfram|Alpha

More things to try:

riemann hypothesis
12! / (4! * 6! * 2!)
Gamma(z)*Gamma(1-z)

Cite this as:

Goodman, Len and Weisstein, Eric W. "Riemann Hypothesis." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/RiemannHypothesis.html

Subject classifications

July 1, 2024

The Biggest Problem in Mathematics Is Finally a Step Closer to Being Solved

Number theorists have been trying to prove a conjecture about the distribution of prime numbers for more than 160 years

By Manon Bischoff

Abstract purple lines funnelling towards the right with white dotted light sources becoming smaller towards the right.

Weiquan Lin/Getty Images

The Riemann hypothesis is the most important open question in number theory—if not all of mathematics. It has occupied experts for more than 160 years. And the problem appeared both in mathematician David Hilbert’s groundbreaking speech from 1900 and among the “Millennium Problems” formulated a century later. The person who solves it will win a million-dollar prize.

But the Riemann hypothesis is a tough nut to crack. Despite decades of effort, the interest of many experts and the cash reward, there has been little progress. Now mathematicians Larry Guth of the Massachusetts Institute of Technology and James Maynard of the University of Oxford have posted a sensational new finding on the preprint server arXiv.org. In the paper, “the authors improve a result that seemed insurmountable for more than 50 years,” says number theorist Valentin Blomer of the University of Bonn in Germany.

Other experts agree. The work is “a remarkable breakthrough,” mathematician and Fields Medalist Terence Tao wrote on Mastodon , “though still very far from fully resolving this conjecture.”

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

The Riemann hypothesis concerns the basic building blocks of natural numbers: prime numbers, values greater than 1 that are only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, 13, and so on.*

Every other number, such as 15, can be clearly broken down into a product of prime numbers: 15 = 3 x 5. The problem is that the prime numbers do not seem to follow a simple pattern and instead appear randomly among the natural numbers. Nineteenth-century German mathematician Bernhard Riemann proposed a way to deal with this peculiarity that explains how prime numbers are distributed on the number line—at least from a statistical point of view.

A Periodic Table for Numbers

Proving this conjecture would provide mathematicians with nothing less than a kind of “periodic table of numbers.” Just as the basic building blocks of matter (such as quarks, electrons and photons) help us to understand the universe and our world, prime numbers also play an important role, not just in number theory but in almost all areas of mathematics.

There are now numerous theorems based on the Riemann conjecture. Proof of this conjecture would prove many other theorems as well—yet another incentive to tackle this stubborn problem.

Interest in prime numbers goes back thousands of years. Euclid proved as early as 300 B.C.E. that there are an infinite number of prime numbers. And although interest in prime numbers persisted, it was not until the 18th century that any further significant findings were made about these basic building blocks.

As a 15-year-old, physicist Carl Friedrich Gauss realized that the number of prime numbers decreases along the number line. His so-called prime number theorem (not proven until 100 years later) states that approximately n / ln( n ) prime numbers appear in the interval from 0 to n . In other words, the prime number theorem offers mathematicians a way of estimating the typical distribution of primes along a chunk of the number line.

The exact number of prime numbers may differ from the estimate given by the theorem, however. For example: According to the prime number theorem, there are approximately 100 / ln(100) ≈ 22 prime numbers in the interval between 1 and 100. But in reality there are 25. There is therefore a deviation of 3. This is where the Riemann hypothesis comes in. This hypothesis gives mathematicians a way to estimate the deviation. More specifically, it states that this deviation cannot become arbitrarily large but instead must scale at most with the square root of n , the length of the interval under consideration.

The Riemann hypothesis therefore does not predict exactly where prime numbers are located but posits that their appearance on the number line follows certain rules. According to the Riemann hypothesis, the density of primes decreases according to the prime number theorem, and the primes are evenly distributed according to this density. This means that there are no large areas in which there are no prime numbers at all, while others are full of them.

You can also imagine this idea by thinking about the distribution of molecules in the air of a room: the overall density on the floor is somewhat higher than on the ceiling, but the particles—following this density distribution—are nonetheless evenly scattered, and there is no vacuum anywhere.

A Strange Connection

Riemann formulated the conjecture named after him in 1859, in a slim, six-page publication (his only contribution to the field of number theory). At first glance, however, his work has little to do with prime numbers.

He dealt with a specific function, the so-called zeta function ζ( s ), an infinitely long sum that adds the reciprocal values of natural numbers that are raised to the power of s :

Even before Riemann’s work, experts knew that such zeta functions are related to prime numbers. Thus, the zeta function can also be expressed as a function of all prime numbers p as follows:

The zeta function as a function of all prime numbers

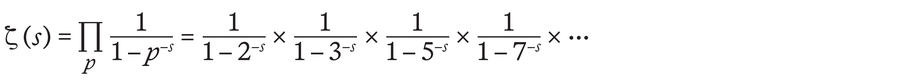
Riemann recognized the full significance of this connection with prime numbers when he used not only real values for s but also complex numbers. These numbers contain both a real part and roots from negative numbers, the so-called imaginary part.

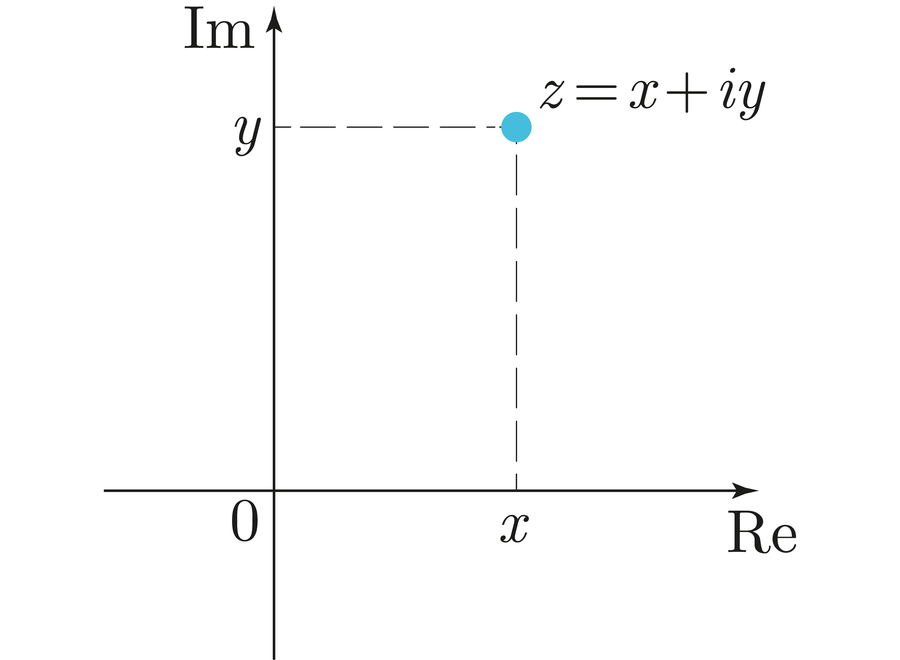
You can imagine complex numbers as a two-dimensional construct. Rather than mark a point on the number line, they instead lie on the plane. The x coordinate corresponds to the real part and the y coordinate to the imaginary part:

The coordinates of z = x + iy illustrate a complex number

Никита Воробьев/Wikimedia

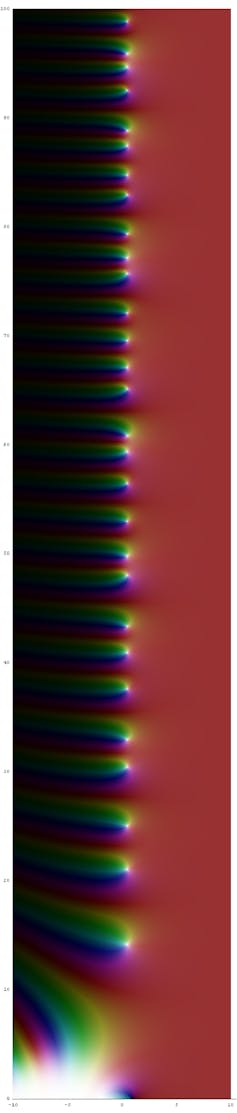
The complex zeta function that Riemann investigated can be visualized as a landscape above the plane. As it turns out, there are certain points amid the mountains and valleys that play an important role in relation to prime numbers. These are the points at which the zeta function becomes zero (so-called zeros), where the landscape sinks to sea level, so to speak.

A visual mapping of the zeta function looks like a mountainscape with peaks and troughs

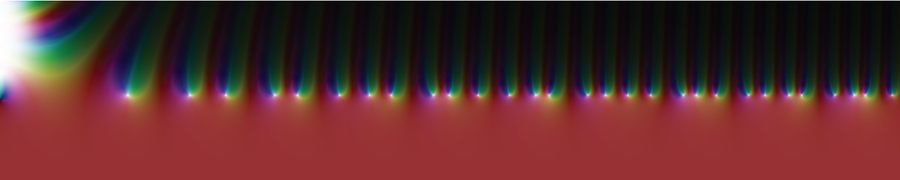
The colors represent the values of the complex zeta function, with the white dots indicating its zeros.

Jan Homann/Wikimedia

Riemann quickly found that the zeta function has no zeros if the real part is greater than 1. This means that the area of the landscape to the right of the straight line x = 1 never sinks to sea level. The zeros of the zeta function are also known for negative values of the real part. They lie on the real axis at x = –2, –4, –6, and so on. But what really interested Riemann—and all mathematicians since—were the zeros of the zeta function in the “critical strip” between 0 ≤ x ≤ 1.

The dark blue area demarcates a stretch along the x axis where the Riemann zeta function contains nontrivial zeros

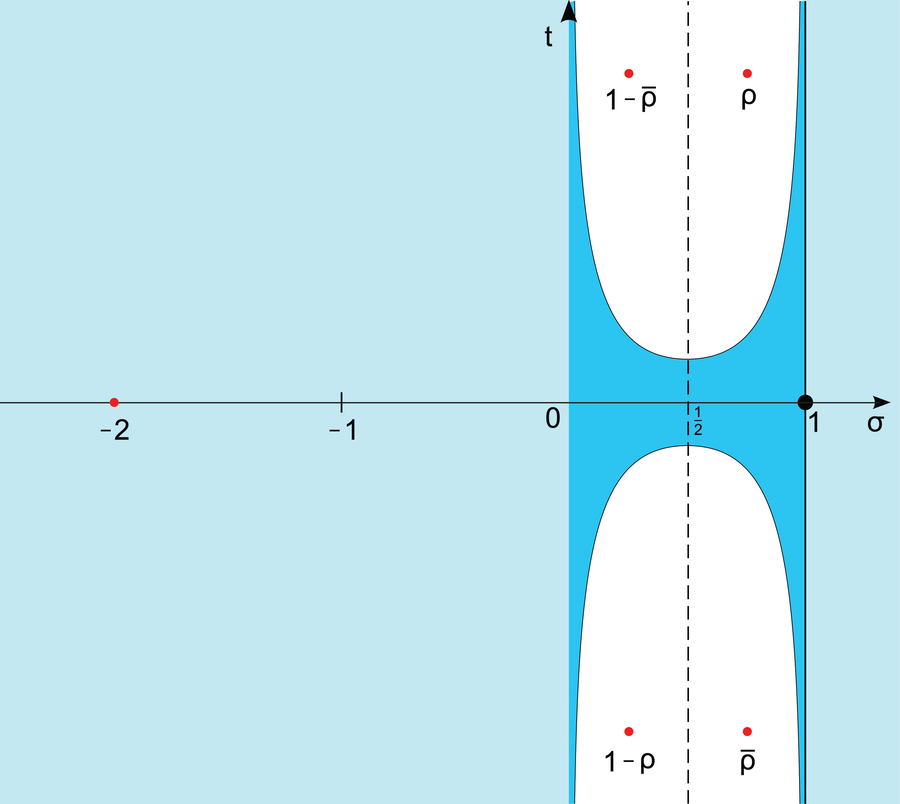
In the critical strip (dark blue), the Riemann zeta function can have “nontrivial” zeros. The Riemann conjecture states that these are located exclusively on the line x = 1/2 (dashed line).

LoStrangolatore/Wikimedia ( CC BY-SA 3.0 )

Riemann knew that the zeta function has an infinite number of zeros within the critical strip. But interestingly, all appear to lie on the straight line x = 1 / 2 . Thus Riemann hypothesized that all zeros of the zeta function within the critical strip have a real part of x = 1 / 2 . That statement is actually at the crux of understanding the distribution of prime numbers. If correct, then the placement of prime numbers along the number line never deviates too much from the prime number set.

On the Hunt for Zeros

To date, billions and billions of zeta function zeros have now been examined— more than 10 13 of them —and all lie on the straight line x = 1 / 2 .

But that alone is not a valid proof. You would only have to find a single zero that deviates from this scheme to disprove the Riemann hypothesis. Therefore we are looking for a proof that clearly demonstrates that there are no zeros outside x = 1 / 2 in the critical strip.

Thus far, such a proof has been out of reach, so researchers took a different approach. They tried to show that there is, at most, a certain number N of zeros outside this straight line x = 1 / 2 . The hope is to reduce N until N = 0 at some point, thereby proving the Riemann conjecture. Unfortunately, this path also turns out to be extremely difficult. In 1940 mathematician Albert Ingham was able to show that between 0.75 ≤ x ≤ 1 there are at most y 3/5+ c zeros with an imaginary part of at most y , where c is a constant between 0 and 9.

In the following 80 years, this estimation barely improved. The last notable progress came from mathematician Martin Huxley in 1972 . “This has limited us from doing many things in analytic number theory,” Tao wrote in his social media post . For example, if you wanted to apply the prime number theorem to short intervals of the type [ x , x + x θ ], you were limited by Ingham’s estimate to θ > 1 / 6 .

Yet if Riemann’s conjecture is true, then the prime number theorem applies to any interval (or θ = 0), no matter how small (because [ x , x + x θ ] = [ x , x + 1] applies to θ = 0).

Now Maynard, who was awarded the prestigious Fields Medal in 2022 , and Guth have succeeded in significantly improving Ingham’s estimate for the first time. According to their work, the zeta function in the range 0.75 ≤ x ≤ 1 has at most y (13/25)+ c zeros with an imaginary part of at most y . What does that mean exactly? Blomer explains: “The authors show in a quantitative sense that zeros of the Riemann zeta function become rarer the further away they are from the critical straight line. In other words, the worse the possible violations of the Riemann conjecture are, the more rarely they would occur.”

“This propagates to many corresponding improvements in analytic number theory,” Tao wrote . It makes it possible to reduce the size of the intervals for which the prime number theorem applies. The theorem is valid for [ x , x + x 2/15 ], so θ > 1 / 6 = 0.166... becomes θ > 2 ⁄ 15 = 0.133...

For this advance, Maynard and Guth initially used well-known methods from Fourier analysis for their result. These are similar techniques to what is used to break down a sound into its overtones. “The first few steps are standard, and many analytic number theorists, including myself, who have attempted to break the Ingham bound, will recognize them,” Tao explained . From there, however, Maynard and Guth “do a number of clever and unexpected maneuvers,” Tao wrote.

Blomer agrees. “The work provides a whole new set of ideas that—as the authors rightly say—can probably be applied to other problems. From a research point of view, that’s the most decisive contribution of the work,” he says.

So even if Maynard and Guth have not solved Riemann’s conjecture, they have at least provided new food for thought to tackle the 160-year-old puzzle. And who knows—perhaps their efforts hold the key to finally cracking the conjecture.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

*Editor’s Note (7/9/24): This sentence was edited after posting to better clarify that prime numbers exclude 1.

Has one of math’s greatest mysteries, the Riemann hypothesis, finally been solved?

Professor of Mathematics, University of Richmond

Disclosure statement

William Ross does not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and has disclosed no relevant affiliations beyond their academic appointment.

University of Richmond provides funding as a member of The Conversation US.

View all partners

Over the past few days, the mathematics world has been abuzz over the news that Sir Michael Atiyah, the famous Fields Medalist and Abel Prize winner, claims to have solved the Riemann hypothesis .

If his proof turns out to be correct, this would be one of the most important mathematical achievements in many years. In fact, this would be one of the biggest results in mathematics, comparable to the proof of Fermat’s Last Theorem from 1994 and the proof of the Poincare Conjecture from 2002 .

Besides being one of the great unsolved problems in mathematics and therefore garnishing glory for the person who solves it, the Riemann hypothesis is one of the Clay Mathematics Institute’s “Million Dollar Problems.” A solution would certainly yield a pretty profitable haul: one million dollars.

The Riemann hypothesis has to do with the distribution of the prime numbers, those integers that can be divided only by themselves and one, like 3, 5, 7, 11 and so on. We know from the Greeks that there are infinitely many primes. What we don’t know is how they are distributed within the integers.

The problem originated in estimating the so-called “prime pi” function, an equation to find the number of primes less than a given number. But its modern reformulation, by German mathematician Bernhard Riemann in 1858, has to do with the location of the zeros of what is now known as the Riemann zeta function.

The technical statement of the Riemann hypothesis is “the zeros of the Riemann zeta function which lie in the critical strip must lie on the critical line.” Even understanding that statement involves graduate-level mathematics courses in complex analysis.

Most mathematicians believe that the Riemann hypothesis is indeed true. Calculations so far have not yielded any misbehaving zeros that do not lie in the critical line. However, there are infinitely many of these zeros to check, and so a computer calculation will not verify all that much. Only an abstract proof will do.

If, in fact, the Riemann hypothesis were not true, then mathematicians’ current thinking about the distribution of the prime numbers would be way off, and we would need to seriously rethink the primes.

The Riemann hypothesis has been examined for over a century and a half by some of the greatest names in mathematics and is not the sort of problem that an inexperienced math student can play around with in his or her spare time. Attempts at verifying it involve many very deep tools from complex analysis and are usually very serious ones done by some of the best names in mathematics.

Atiyah gave a lecture in Germany on Sept. 25 in which he presented an outline of his approach to verify the Riemann hypothesis. This outline is often the first announcement of the solution but should not be taken that the problem has been solved – far from it. For mathematicians like me, the “proof is in the pudding,” and there are many steps that need to be taken before the community will pronounce Atiyah’s solution as correct. First, he will have to circulate a manuscript detailing his solution. Then, there is the painstaking task of verifying his proof. This could take quite a lot of time, maybe months or even years.

Is Atiyah’s attempt at the Riemann hypothesis serious? Perhaps. His reputation is stellar, and he is certainly capable enough to pull it off. On the other hand, there have been several other serious attempts at this problem that did not pan out. At some point, Atiyah will need to circulate a manuscript that experts can check with a fine-tooth comb.

Mathematics
Prime numbers
Quick reads

Manager, Regional Training Hub

Head of Evidence to Action

Supply Chain - Assistant/Associate Professor (Tenure-Track)

OzGrav Postdoctoral Research Fellow

Casual Facilitator: GERRIC Student Programs - Arts, Design and Architecture

Riemann Hypothesis

$1/2$

Some equivalent statements of the Riemann Hypothesis are

$\frac{1}{2}$

Purported Disproof of the Mertens Conjecture

Number theory

Something appears to not have loaded correctly.

Click to refresh .

A Primer on the Riemann Hypothesis

First Online: 15 September 2023

Cite this chapter

Michael E. N. Tschaffon 21 ,
Iva Tkáčová 22 ,
Helmut Maier 23 &
Wolfgang P. Schleich 24 , 25

Part of the book series: Lecture Notes in Physics ((LNP,volume 1000))

594 Accesses

We provide an introduction for physicists into the Riemann Hypothesis. For this purpose, we first introduce, and then compare and contrast the Riemann function and the Dirichlet L-functions, with the Titchmarsh counterexample. Whereas the first two classes of functions are expected to satisfy the Riemann Hypothesis, the Titchmarsh counterexample is known to violate it. Throughout our article we employ elementary mathematical techniques known to every physicist. Needless to say, we do not verify the Riemann Hypothesis but suggest heuristic arguments in favor of it. We also build a bridge to quantum mechanics by interpreting the Dirichlet series central to this field as a superposition of probability amplitudes leading us to an unusual potential with a logarithmic energy spectrum opening the possibility of factoring numbers.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

Get 10 units per month
Download Article/Chapter or eBook
1 Unit = 1 Article or 1 Chapter
Cancel anytime
Available as PDF
Read on any device
Instant download
Own it forever
Available as EPUB and PDF
Compact, lightweight edition
Dispatched in 3 to 5 business days
Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

M. Abramowitz, I.A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables , vol. 55 (US Government Printing Office, Washington, 1948)

MATH Google Scholar

C.M. Bender, D.C. Brody, M.P. Müller, Hamiltonian for the zeros of the Riemann zeta function. Phys. Rev. Lett. 118 (13), 130201 (2017)

Google Scholar

M.V. Berry, J.P. Keating, A new asymptotic representation for $\zeta $ ( $1/2$ + it) and quantum spectral determinants. Proc. R. Soc. Lond. A Math. Phys. Sci. 437 (1899), 151–173 (1992)

M.V. Berry, J.P. Keating, The Riemann zeros and eigenvalue asymptotics. SIAM Rev. 41 (2), 236–266 (1999)

Article ADS MathSciNet MATH Google Scholar

P. Borwein, S. Choi, B. Rooney, A. Weirathmueller, The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike . CMS Books in Mathematics Series (Springer, New York, 2008)

D. Cassettari, G. Mussardo, A. Trombettoni, Holographic realization of the prime number quantum potential. PNAS Nexus 2 (1), 1–9 (2022)

M. Du Sautoy, The Music of the Primes (Harper Collins, New York, 2003)

H.M. Edwards, Riemann’s Zeta Function (Academic, New York, 1974)

W.J. Ellison, F. Ellison, Prime Numbers (Wiley, New York, 1985)

C. Feiler, W.P. Schleich, Entanglement and analytical continuation: an intimate relation told by the Riemann zeta function. New J. Phys. 15 (6), 063009 (2013)

C. Feiler, W.P. Schleich, Dirichlet series as interfering probability amplitudes for quantum measurements. New J. Phys. 17 (6), 063040 (2015)

G. Freiling, V.A. Yurko, Inverse Sturm-Liouville Problems and Their Applications (NOVA Science Publishers, Huntington, 2001)

F. Gleisberg, W.P. Schleich, Factorization with a logarithmic energy spectrum of a central potential. Acta Phys. Pol. A 143 , S112 (2023)

Article ADS Google Scholar

F. Gleisberg, R. Mack, K. Vogel, W.P. Schleich, Factorization with a logarithmic energy spectrum. New J. Phys. 15 (2), 023037 (2013)

F. Gleisberg, M. Volpp, W.P. Schleich, Factorization with a logarithmic energy spectrum of a two-dimensional potential. Phys. Lett. A 379 (40–41), 2556–2560 (2015)

Article ADS MATH Google Scholar

F. Gleisberg, F. Di Pumpo, G. Wolff, W.P. Schleich, Prime factorization of arbitrary integers with a logarithmic energy spectrum. J. Phys. B 51 (3), 035009 (2018)

I.S. Gradstein, I.M. Ryzhik, Tables of Integrals, Sums, Series and Products (Academic Press, New York, 1994)

R. Grimm, M. Weidemüller, Y.B. Ovchinnikov, Optical dipole traps for neutral atoms. Adv. Atom. Mol. Opt. Phys. 42 , 95–170 (2000)

D. Hilbert, Mathematische Probleme. Arch. Math. Phys. 1 , 44–63 and 213–237 (1901). English translation by Mary Newson. Bull. Am. Math. Soc. 8 , 437–479 (1901)

H. Iwaniec, E. Kowalski, Analytic Number Theory (American Mathematical Society, Providence, 2003)

B.M. Levitan, Inverse Sturm-Liouville Problems (VNK Science Press, Utrecht, 1987)

Book MATH Google Scholar

R. Mack, J.P. Dahl, H. Moya-Cessa, W.T. Strunz, R. Walser, W.P. Schleich, Riemann $\zeta $ function from wave packet dynamics. Phys. Rev. A 82 (3), 032119 (2010)

G.E. Mitchell, A. Richter, H.A. Weidenmüller, Random matrices and chaos in nuclear physics: nuclear reactions. Rev. Mod. Phys. 82 (4), 2845 (2010)

J.W. Neuberger, C. Feiler, H. Maier, W.P. Schleich, Newton flow of the Riemann zeta function: separatrices control the appearance of zeros. New J. Phys. 16 , 103023 (2014)

J.W. Neuberger, C. Feiler, H. Maier, W.P. Schleich, The Riemann hypothesis illuminated by the Newton flow of $\zeta $ . Phys. Scr. 90 , 108015 (2015)

B Riemann, Monatsberichte der Berliner Akademie (1859). Transcribed German version and English translation by D. R. Wilkins see http://www.claymath.org/publications/riemanns-1859-manuscript

D. Rockmore, Stalking the Riemann Hypothesis: The Quest to Find the Hidden Law of Prime Numbers (Pantheon Books, New York, 2005)

K. Sabbagh, The Riemann Hypothesis: The Greatest Unsolved Problem in Mathematics (Farar, Straus and Giroux, New York, 2003)

W.P. Schleich, Quantum Optics in Phase Space (VCH-Wiley, Weinheim, 2001)

W.P. Schleich, I. Bezdĕková, M.B. Kim, P.C. Abbott, H. Maier, H.L. Montgomery, J.W. Neuberger, Equivalent formulations of the Riemann Hypothesis based on lines of constant phase. Phys. Scr. 93 , 065201 (2018)

D. Schumayer, D.A.W. Hutchinson, Physics of the Riemann hypothesis. Rev. Mod. Phys. 83 (2), 307 (2011)

C.L. Siegel, Über Riemanns Nachlaß zur analytischen Zahlentheorie. Quellen Stud. Geschichte Math. Astron. Phys. Abt. B: Stad 2 (1932), p. 45

R. Spira, Some zeros of the Titchmarsh counterexample. Math. Comput. 63 , 747–748 (1994)

E.C. Titchmarsh, The Theory of the Riemann Zeta-Function (Clarendon Press, Oxford, 1967)

J. Twamley, G.J. Milburn, The quantum Mellin transform. New J. Phys. 8 (12), 328 (2006)

F. Ullinger, M. Zimmermann, W.P. Schleich, The logarithmic phase singularity in the inverted harmonic oscillator. AVS Quantum Sci. 4 (2), 024402 (2022)

J.A. Wheeler, in Studies in Mathematical Physics: Essays in Honor of Valentine Bargmann . ed. by E.H. Lieb, B. Simon, A.S. Wightman (Princeton University Press, Princeton, 1976)

E.T. Whittaker, G.N. Watson, A Course of Modern Analysis (Cambridge University Press, Cambridge, 1996)

M. Wolf, Will a physicist prove the Riemann Hypothesis? Rep. Prog. Phys. 83 (3), 036001 (2020)

Download references

Acknowledgements

We thank P. C. Abbott, M. B. Kim, H. L. Montgomery, J. W. Neuberger, M. Zimmermann for many fruitful discussions, E. P. Glasbrenner for technical assistance and J. Pohl for her help with the scans of Riemann’s article. Moreover, we are most grateful to the Niedersächsische Staats- und Universitätsbibliothek and, in particular, R. B. Röper for allowing us to present excerpts of Riemann’s original manuscript. W. P. S. is also grateful to Texas A & M University for a Faculty Fellowship at the Hagler Institute for Advanced Study at Texas A& M University and to Texas A& M AgriLife for the support of this work. The research of the IQST is financially supported by the Ministry of Science, Research and Arts Baden-Württemberg. I. B. is grateful for the financial support from the Technical University of Ostrava, Grant No. SP2018/44.

Author information

Authors and affiliations.

Institut für Quantenphysik and Center for Integrated Quantum Science and Technology (IQST), Universität Ulm, Ulm, Germany

Michael E. N. Tschaffon

Department of Physics, Faculty of Electrical Engineering and Computer Science, VSB-Technical University of Ostrava, Ostrava, Poruba, Czech Republic

Iva Tkáčová

Institut für Reine Mathematik, Universität Ulm, Ulm, Germany

Helmut Maier

Wolfgang P. Schleich

Hagler Institute for Advanced Study, Institute for Quantum Science and Engineering (IQSE), and Texas A&M AgriLife Research, Texas A&M University, College Station, TX, USA

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael E. N. Tschaffon .

Editor information

Editors and affiliations.

Department of Physics “E.R.Caianiello”, University of Salerno, Fisciano, Italy

Roberta Citro

Quantum Optics Theory, Institute of Photonic Sciences, Castelldefels (Barcelona), Spain

Maciej Lewenstein

Theory Department, Max Planck Institute for the Structure and Dynamics of Matter, Hamburg, Germany

Angel Rubio

Institute of Quantum Physics, University of Ulm, Ulm, Germany

Physics Department, University of Michigan–Ann Arbor, Ann Arbor, MI, USA

James D. Wells

CSPAR & SPA, University of Alabama in Huntsville, Huntsville, AL, USA

Gary P. Zank

Appendix 1: Functional Equation of Jacobi Theta Function

In this Appendix we briefly rederive the functional equation, Eq. ( 26 ), of the Jacobi theta function

defined by Eq. ( 21 ), in order to bring out most clearly the origin of the difference to the corresponding relation, Eq. ( 155 ), for the generalized Jacobi theta function given by Eq. ( 154 ).

Since the summation index n appears in $\omega $ as a square, we can immediately include negative values of n together with a factor of $1/2$ . However, the term corresponding to $n=0$ is unity. Thus, we have to subtract this contribution, and arrive at the representation

of $\omega $ .

Next we employ the Poisson summation formula

where $b=b(\nu )$ is a continuous extension of the discrete coefficients $b_n$ . We emphasize that the specific form of the extension is of no consequence as long as $b(n)\equiv b_n$ .

Indeed, this fact is a result of the identity

which is at the very heart of the Poisson summation formula.

For the choice

and with the help of the integral relation

we arrive at the identity

which leads us with the representation, Eq. ( 195 ), of $\omega $ to

that is, the familiar functional equation

We emphasize that the second term in Eq. ( 202 ), which is independent of $\omega $ , is a consequence of the absence of the term $n=0$ in the definition, Eq. ( 194 ), of the Jacobi theta function $\omega $ leading to the subtraction of unity in Eq. ( 195 ).

Appendix 2: Equivalent Condition for Non-trivial Zeros

In Sect. 2.4 we have derived the condition, Eq. ( 39 ) , for a zero on the critical line given by the identity of an integral

containing an oscillatory integrand with a Lorentzian. We devote this appendix to the derivation of an alternative but equivalent formulation by casting the integral into a different form.

In particular, we analyze the asymptotic behavior of J . For this purpose, we first derive an exact alternative expression for J , and then consider the limit $\tau \rightarrow \infty $ .

We start by introducing in J the new integration variable $y\equiv (1/2)\ln x$ , or $x=\exp (2y)$ , which with the identity $\mathrm {d}y=\mathrm {d}x/(2x)$ leads us to the form

Next, we obtain by integration by parts the equivalent representation

where we have used the fact that the boundary terms vanish, and find performing the differentiation

Finally, we introduce the new integration variable $\theta \equiv \tau y$ , and arrive at the expression

When we recall from Eq. ( 21 ) the definition

of $\omega $ , the differentiation yields the explicit formula

which decays for increasing $\tau $ as $1/ \tau ^2$ which is identical to the decrease of the Lorentzian on the right-hand side of Eq. ( 39 ).

When we now compare this representation of J to the initial one, Eq. ( 203 ), we find, apart from the decay with $1/\tau ^2$ , three distinct features: (i) The oscillatory function in the integral is independent of $\tau $ . (ii) We have a double-exponential decay, but (iii) this rapid decay only sets in for integration variables $\theta > \tau /2$ .

Hence, the expression, Eq. ( 209 ), for J shows that the main contribution to this integral results from the decays characterized by the summation index n that are fast compared to the oscillation period, in complete agreement with the discussion of Sect. 2.4 .

Appendix 3: Exponential Product

In this appendix we cast the product

where q is an integer and $\kappa =0,1$ , into an exponential form, which allows us to derive in a straight-forward way an asymptotic limit of $\lambda $ . This term is not only a factor in the definition, Eq. ( 151 ), of the Dirichlet L-function $\Lambda $ but also appears in the Riemann function $\xi $ , defined by Eq. ( 40 ) for the special case $q=1$ and $\kappa =0$ .

We first derive a general expression for $\lambda $ and then perform the asymptotic limit. Finally, we address the special case of the Riemann function.

1.1 General Expression

We start from the definition, Eq. ( 210 ), of $\lambda $ in the exponential form

and recall the representation [ 17 ]

of the logarithm of the Gamma function with the remainder

which leads us for the argument $(s+\kappa )/2$ to the expression

Here we have introduced the abbreviation

and $\bar {R}$ is defined by Eq. ( 213 ).

1.2 Asymptotic Limit

Next we consider the limit $s \rightarrow \infty $ . In this case we find with the help of the expansion

the relation

Moreover, the generating function [ 1 ]

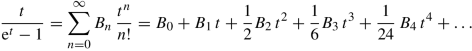
of the Bernoulli numbers $B_n$ with

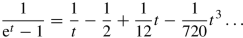
allows us to expand the remainder $\bar {R}$ given by Eq. ( 213 ) into inverse powers of s with the leading contribution

Hence, we arrive in the lowest order of $1/s$ at the asymptotic expression

for $\mathcal {R}$ , which apart from the constant term decays as $1/s$ .

1.3 Special Case: Riemann Function

Finally, we discuss the example $q=1$ and $\kappa =0$ corresponding to the Riemann function $\xi $ . In this case, Eq. ( 214 ) reduces to

where $\mathcal {R}$ given by Eq. ( 215 ) simplifies to

With the help of the asymptotic limit Eq. ( 221 ), we find the expression

for the remainder, which together with Eq. ( 224 ) is consistent with Eq. ( 222 ) for $\kappa =0$ .

Appendix 4: Lines of Constant Height and Constant Phase

In Sect. 3.6.3 we have derived an asymptotic expression for $\xi $ which arises solely from the product $(\wp /2)\pi ^{-s/2}\Gamma \left (s/2\right )$ since we have made the approximation $\zeta =1$ . This formula is in terms of the complex variable s .

In this appendix, we first cast this expression in terms of amplitude and phase, and then consider two special cases. We conclude by verifying these approximations using the Cauchy-Riemann differential equations in amplitude and phase discussed in the Chapter “Insights into Complex Functions” of this volume.

1.1 Decomposition in Amplitude and Phase

We start by decomposing the approximation

of $\alpha _{\xi }$ into its real and imaginary parts $\Sigma $ and $\Phi $ , that is,

determining the absolute value

and the phase $\Phi $ of $\xi $ . Here, we first derive general expressions for $\Sigma $ and $\Phi $ , and then consider the two extreme limits $1<\sigma \ll \tau $ and $0\leq \tau \ll \sigma $ .

With the identity

leading us to

we find the explicit expressions

We emphasize that the decomposition, Eq. ( 227 ), of the approximation, Eq. ( 226 ), of $\alpha _{\xi }$ into $\Sigma $ and $\Phi $ given by Eqs. ( 231 ) and ( 232 ) is exact.

1.2 Special Limits

In order to gain insight into the dependence of $\Sigma $ and $\Phi $ on $\sigma $ and $\tau $ , we now consider two extreme limits, and derive approximate but analytic expressions for $\Sigma $ and $\Phi $ .

1.2.1 At the Center of the Complex Plane

We start with the case of $1<\sigma \ll \tau $ , and arrive with the help of the approximations

at the expressions

In this limit, the lines $\tau _{\Phi } = \tau _{\Phi }(\sigma )$ of constant phase $\Phi $ satisfy an interesting symmetry relation. Indeed, for a given value $\tau $ the lines of constant phase corresponding to $\Phi $ and $\Phi +\pi $ are separated in their values of $\sigma $ and $\sigma ^{\prime }$ by 4. This property follows from Eq. ( 237 ) which for $\Phi +\pi $ reads

and a comparison with Eq. ( 237 ) immediately yields the connection

and thus the identity

Next, we derive an explicit expression for $\tau _{\Phi }$ . Unfortunately, Eq. ( 237 ) is a transcendental equation, that is, the Lambert equation, and cannot be solved directly. However, in the limit of large $\tau $ we obtain an approximate expression for $\tau _{\Phi }$ by iteration.

For this purpose, we first cast Eq. ( 237 ) into the form

and replace $\tau _{\Phi }$ in the slowly varying logarithm by the right-hand side leading us to the formula

We conclude by noting that this expression obviously also satisfies the periodicity property, Eq. ( 240 ).

1.2.2 At the Right Edge of the Complex Plane

Next we consider the case $0\leq \tau \ll \sigma $ and arrive with

In this limit $\Sigma $ , and thus $|\xi |$ grows exponentially with $\sigma \ln (\sigma /2\pi )$ for increasing $\sigma $ , but decays like a Gaussian due to the term $-\tau ^2/(4\sigma )$ for $\tau $ increasing from zero. Moreover, $\Phi $ increases linearly with $\tau $ with a rate mainly given by $\ln (\sigma /2\pi )$ .

According to Eq. ( 247 ), in this asymptotic limit the lines $\tau _{\Phi } = \tau _{\Phi }(\sigma )$ of constant phase $\Phi $ read

and decay with a rate, that is, inversely proportional to $\ln (\sigma /(2\pi ))$ . In particular, $\tau = 0$ , that is, the real axis, corresponds to the phase $\Phi = 0$ , and all phase lines approach it as $\sigma \rightarrow \infty $ .

In the last step of Eq. ( 248 ), we have neglected the correction term $3/\sigma $ since in obtaining the general expression, Eq. ( 226 ), of $\alpha _{\xi }$ we have already neglected terms of the order $1/s$ .

1.3 Cauchy-Riemann Differential Equations

Next we probe the consistency of our approximations, Eqs. ( 236 ) and ( 246 ), as well as Eqs. ( 237 ) and ( 247 ) for the amplitude $\Sigma $ as well as the phase $\Phi $ of the exponential representation

of $\xi $ by applying the Cauchy-Riemann differential equations

discussed in the Chapter “Insights into Complex Functions” of this volume.

We start with the asymptotic expressions

obtained in the previous section for $1<\sigma \ll \tau $ .

Indeed, by direct differentiation we find

in complete agreement with the Cauchy-Riemann differential equation, Eq. ( 250 ).

Moreover, we also obtain the result

which is consistent with the expression

that is, with Eq. ( 256 ) when we neglect the terms proportional to $1/\tau $ . Indeed, in the derivation of the expression, Eq. ( 253 ) for $\Phi $ we have already neglected contributions of this order.

Next, we address the approximations

valid for $0\leq \tau \ll \sigma $ , and find immediately

where in the last step we have neglected the term $(\tau /\sigma )^2\ll 1$ . Hence, we have verified the Cauchy-Riemann differential equation, Eq. ( 250 ).

Moreover, we obtain from Eq. ( 258 ) the relation

and Eq. ( 259 ) yields

Hence, we satisfy the Cauchy-Riemann differential equation, Eq. ( 251 ), in the approximation $\sigma \ll 1$ .

Appendix 5: Special Examples of Normalized Gauss Sums

In Sect. 5 we have shown that the normalized Gauss sum

is given by a phase factor whose phase $\beta $ is determined by the Dirichlet character $\chi $ . We now illustrate this result by evaluating the normalized Gauss sum of three different characters.

For this purpose, we first consider the normalized Gauss sums associated with the Dirichlet characters forming the Titchmarsh counterexample. In these examples, the phase is non-vanishing. We then calculate the normalized Gauss sum of a character where the phase does vanish.

1.1 Non-vanishing Phase

We start by evaluating the Gauss sums $G_1$ and $G_2$ corresponding to the characters $\chi _1$ and $\chi _2$ defined $\mathrm {mod}\;5$ with the values

and demonstrate that they are phase factors, in complete accordance with Eq. ( 143 ). Since $\chi _1$ and $\chi _2$ are the complex conjugate of each other, the corresponding phases must satisfy the symmetry relation, Eq. ( 144 ).

We start by noting that in both characters $q=5$ . Thus, we find with $\chi _j(-1) = \chi _j(4-5) = \chi _j(4)$ for $j=1,2$ , and the definitions Eqs. ( 264 ) and ( 265 ) of $\chi _1$ and $\chi _2$ , the result $\chi _1(-1)=\chi _2(-1)=-1$ which yields with Eq. ( 127 ) the parameter

Hence, the Gauss sum $G_1$ , corresponding to the character $\chi _1$ reads

and takes with the help of the definition, Eq. ( 264 ), of $\chi _1$ , the form

where in the last step we have taken advantage of the $2\pi $ -periodicity of the Fourier factors.

In terms of trigonometric functions, we find

and the values

finally yield the expression

for the Gauss sum $G_1$ as a phase factor where

We conclude by briefly addressing the Gauss sum

associated with

Indeed, this symmetry enforces that in $G_2$ the second and the third term in Eq. ( 267 ) change their signs, but everything else remains the same.

As a result, we arrive at a negative rather than a positive phase, that is,

We emphasize that the sign change in the phase due to the transition from $G_1$ to $G_2,$ Eqs. ( 269 ) and ( 272 ), can also be viewed as a consequence of the connection, Eq. ( 271 ), between $\chi _1$ and $\chi _2$ , and the symmetry relation, Eq. ( 144 ).

1.2 Vanishing Phase

We conclude by discussing an example of a character $\chi $ where the phase of the corresponding normalized Gauss sum vanishes. For this purpose, we consider the real-valued character

with an integer k .

Since $\chi $ is $\mathrm {mod} \; 4$ we find $q=4$ and with $\chi (-1) = \chi (3-4)=\chi (3) = -1$ following from the definition, Eq. ( 273 ), of $\chi $ , we obtain with the help of Eq. ( 127 ) the value $\kappa =1.$

Hence, the normalized Gauss sum, Eq. ( 263 ), takes the form

which with the definition, Eq. ( 273 ), of the character $\chi $ reads

For the character $\chi $ , given by Eq. ( 273 ), we obtain indeed a vanishing phase $\beta $ for G .

Appendix 6: Functional Equation of Generalized Jacobi Theta Function

Since the functional equation

of the generalized Jacobi theta function plays a crucial role in the analytic continuation of the Dirichlet L-functions, as discussed in Sect. 6 , we devote the present Appendix to a brief summary of the derivation. This analysis also brings out most clearly the origins of the Gauss sum G and the character in its complex conjugate form.

Here we proceed in two steps: (i) We first show that due to the appearance of the character $\chi $ and the term $n^\kappa $ in the definition of $\omega $ we can express the summation in $\omega $ from unity to infinity, into one from minus infinity to plus infinity by merely introducing a factor $1/2$ . This additional symmetry is the deeper reason for the simplicity of the functional equation, Eq. ( 275 ), of the Jacobi theta function for $\Lambda ,$ compared to the one for $\xi $ . (ii) Next we take advantage of the periodicity of the character together with the Poisson summation formula, and arrive at the functional equation, Eq. ( 275 ), of $\omega $ corresponding to $\Lambda .$

We conclude by briefly comparing the derivation of the functional equation of the Jacobi theta function $\omega $ corresponding to $\Lambda $ to that for $\xi $ . In particular, we show that the origin of the quadratic polynomial $s(s-1)$ and the off-set $1/2$ in the analytic continuation, Eq. ( 43 ), of $\xi $ is the fact that the term $n=0$ in $\omega $ corresponding to $\xi $ is nonzero.

1.1 Extension of Summation

We start by verifying the representation

For this purpose we consider the sum

and decompose S into a sum over all positive, and one over all negative integers including zero, that is,

where in the sum over negative n we have replaced $-n$ by $n.$

When we recall the connection, Eq. ( 128 ), between $\chi (-n)$ and $\chi (n)$ together with $\chi (0) = 0$ , Eq. ( 119 ), we find the expression

The values, Eq.( 127 ), of $\kappa $ together with the relation $\chi (-1) = \pm 1$ yield the identity

and the definition, Eq. ( 277 ), of $\omega $ the desired representation, Eq. ( 276 ).

1.2 Emergence of Gauss Sum

Since the character $\chi $ satisfies the periodicity condition, Eq. ( 116 ), it is useful to apply the summation formula

valid for any appropriately converging sum of coefficients $d(n)$ , to S in the form

where we have introduced the abbreviation

Indeed, with the help of Eq. ( 116 ) we immediately find the representation

of S which with the Poisson summation formula

takes the form

Finally, the new integration variable

yields the expression

where we have interchanged the two summations, and have recalled the definition, Eq. ( 130 ), of the Gauss sum $\tilde {G}(\chi ,m).$

Next we use the reduction formula, Eq. ( 129 ), which allows us to factor $\tilde {G}(\chi ,1)$ out of the sum over m and to find

With the definition of h , Eq. ( 282 ), and the integral formula

we finally arrive at

that is, the functional equation, Eq. ( 275 ), of $\omega $ when we use the relation, Eq. ( 276 ). Moreover, we have recalled the definition, Eq. ( 142 ), of the Gauss sum.

1.3 Comparison to Jacobi Theta Function of $\xi $

We conclude by briefly comparing and contrasting this derivation of the functional equation of the Jacobi theta function of $\Lambda $ to the corresponding one for the Jacobi theta function of $\xi $ , defined by Eq. ( 21 ) and discussed in Appendix 1.

In contrast to the generalized Jacobi theta function, Eq. ( 154 ), where the term $n=0$ vanishes due to $\chi (0)=0$ , Eq. ( 119 ), the contribution in the one for $\xi $ is unity. This difference is important since the term in Eq. ( 202 ) independent of $\omega $ is a consequence of the subtraction of the term $n=0$ in Eq. ( 195 ). As a result, in the corresponding functional equation, Eq. ( 275 ), for the generalized Jacobi theta function only the contribution proportional to $\omega (1/x)$ enters.

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Tschaffon, M.E.N., Tkáčová, I., Maier, H., Schleich, W.P. (2023). A Primer on the Riemann Hypothesis. In: Citro, R., Lewenstein, M., Rubio, A., Schleich, W.P., Wells, J.D., Zank, G.P. (eds) Sketches of Physics. Lecture Notes in Physics, vol 1000. Springer, Cham. https://doi.org/10.1007/978-3-031-32469-7_7

Download citation

DOI : https://doi.org/10.1007/978-3-031-32469-7_7

Published : 15 September 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-32468-0

Online ISBN : 978-3-031-32469-7

eBook Packages : Physics and Astronomy Physics and Astronomy (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Publish with us

Policies and ethics

Find a journal
Track your research

Every print subscription comes with full digital access

Science News

Mathematicians report possible progress on proving the riemann hypothesis.

A new study of Jensen polynomials revives an old approach

STILL ELUSIVE Researchers may have edged closer to a proof of the Riemann hypothesis — a statement about the Riemann zeta function, plotted here — which could help mathematicians understand the quirks of prime numbers.

Jan Homann/Wikimedia Commons

This intricate maze connects the dots on quasicrystal surfaces

$An illustration of bacterial molecules forming a triangular fractal.$

Scientists find a naturally occurring molecule that forms a fractal

An image of grey numbers piled on top of each other. All numbers are grey except for the visible prime numbers of 5, 11, 17, 23 and 29, which are highlighted blue.

How two outsiders tackled the mystery of arithmetic progressions

A predicted quasicrystal is based on the ‘einstein’ tile known as the hat.

The produce section of a grocery store with lots of fruit and vegetables on sloped displays

Here’s how much fruit you can take from a display before it collapses

Here are some astounding scientific firsts of 2023

An image showing 1+1=2 with other numbers fading into the black background.

‘Is Math Real?’ asks simple questions to explore math’s deepest truths

An illustration of a green Möbius strip, a loop of paper with a half-twist in it.

An enduring Möbius strip mystery has finally been solved

Subscribers, enter your e-mail address for full access to the Science News archives and digital editions.

Not a subscriber? Become one now .

The History and Importance of the Riemann Hypothesis

Table of Contents

Riemann Hypothesis History

The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field of number theory. It’s named after the German mathematician Bernhard Riemann, who introduced the hypothesis in 1859.

RH: All non-trivial zeros of the Riemannian zeta function lie on the critical line.
ERH: All zeros of L-functions to complex Dirichlet characters of finite cyclic groups within the critical strip lie on the critical line.
Related Article: The Extended Riemann Hypothesis and Ramanujan’s Sum: Shortest Possible Explanation

The history of the Riemann hypothesis may be considered to start with the first mention of prime numbers in the Rhind Mathematical Papyrus around 1550 BC. It certainly began with the first treatise of prime numbers in Euclid’s Elements in the 3rd century BC. It came to a – hopefully temporary – end on the 8th of August 1900 on the list of Hilbert’s famous problems. And primes are the reason why we are more than ever interested in the question of whether ERH holds or not. E.g. the RSA encryption algorithm (Rivest-Shamir-Adleman, 1977) relies on the complexity of the factorization problem FP, that it is NP-hard. FP is probably neither NP-complete nor in P but we do not know for sure. Early factorization algorithms that ran in a reasonable time had to assume the extended Riemann hypothesis (Lenstra, 1988, [1]). So what do prime numbers have in common with the Riemann hypothesis which is about a function defined as a Dirichlet series? $$ \zeta(s)=\sum_{n=1}^\infty \dfrac{1}{n^s} $$ One has to admit that what we call prime number theory today originated in the 19th century when Dirichlet began in 1837 to apply analysis to number theory. There is a large gap between Euclid and Euler who published a new proof for the infinite number of primes in 1737.

Prime Numbers

A short answer would be that $$ \zeta(s)=\sum_{n=1}^\infty \dfrac{1}{n^s}=\prod_{p\text{ prime}}\dfrac{1}{1-{p}^{-s}}. $$ This is easy to prove [5] but falls a bit short of the relationship between prime numbers and the Riemann hypothesis. E.g. the basic idea for our example of why FP can be solved quickly under the assumption of ERH is, that ERH implies the existence of relatively small primes which then can be found by fast algorithms. (See the theorems of Ankeney/Montgomery/Bach, Miller, Bach [10] and the references therein.)

Let ##1/2 \leq \theta \leq 1.## Then

$$\large{\operatorname{RH}(\theta)\, : \,\zeta(s) \text{ has no zeros in }\{\mathfrak{R}(s)>\theta\}}$$

is another generalization of the Riemann hypothesis. The original Riemann hypothesis is thus ##\operatorname{RH}(1/2)## and we know there are no zeros of the zeta-function in ##\{\mathfrak{R}(s)>1\}##. So ##\operatorname{RH}(1)## is true, but no proof is known for values of ##\theta## below. We do know ([7],[8],[9]) that $$ \large{\operatorname{RH}(\theta)\quad \Longleftrightarrow\quad \pi(x)=\operatorname{Li}(x) + O\left(x^{\theta +\varepsilon }\right)\text{ for all }\varepsilon >0} $$ where ##\operatorname{Li}(x)=\displaystyle{\int_2^x \dfrac{dt}{\log t}}## is the integral logarithm and ##\pi(x)=\left|\{p\in \mathbb{P}\,|\,p\leq x\}\right|## the prime number function (graphic from [2]). Hence ERH is connected to the question: Where are the primes?

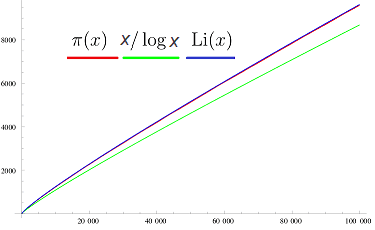
The prime number theorem $$ \lim_{x \to \infty}\dfrac{\pi(x)}{\dfrac{x}{\log(x)}}=1 $$ was first conjectured by Gauß in 1792, however, proven by Hadamard and de la Vallée-Poussin independently a hundred years later in 1896. Their proofs were of function theoretical nature and relied on the relation of primes to the Riemannian ##\zeta##-function which was first considered by Euler in the 18th century.

Another interesting equivalent formulation of ##\operatorname{RH}(\theta)## is the following: Let ##a_{even}## be the number of integers below ##x>0## that are a product of an even number of primes, and ##a_{odd}## be the number of integers below ##x>0## that is a product of an odd number of primes, then $$ \large{\operatorname{RH}(\theta)\quad \Longleftrightarrow\quad a_{even}(x)-a_{odd}(x) = O\left(x^{\theta +\varepsilon }\right)\text{ for all }\varepsilon >0.} $$ These two equations show that the Riemann hypothesis is not only about a Dirichlet series, or the safety of some encryption algorithms. It is why I said it all began with the notion of prime numbers. We simply want to know how prime numbers are distributed. History shows that we are fascinated by prime numbers. The Riemann hypothesis ##\operatorname{RH}(1/2)## is meanwhile checked for the first ##10,000,000,000,000## zeros of the ##\zeta##-function [11], i.e. any other result than its truth would be more than surprising. In the end, we can check as many zeros as our computers can handle, it will never be a proof. However, these results above marked a huge step in the theory of prime numbers. It wasn’t long before when Euler (1707 – 1783) wrote:

“Mathematicians have hitherto strove in vain to discover any order in the sequence of prime numbers, and one is inclined to believe that this is a mystery which the human mind will never fathom. To convince oneself of this, one need only glance at the prime number tables, which some have taken the trouble to extend to 100,000, and one will at first notice that there is no order, no rule to be observed.” [12]

Early Glory

Riemann’s conjecture was only incidentally mentioned by Riemann himself, and not explicitly identified as an important problem. Riemann wrote about the zeros:

“One finds many roots within these limits, and, probably, all the roots are there. Of course, rigorous proof of this would be desirable; however, after a few unsuccessful attempts, I have left the search for it aside for the time being, since it seems unnecessary for my investigation.”

Nevertheless, he has proven that there are infinitely many roots ##s## of the ##\zeta##-function with ##\mathfrak{R}(s)=1/2## and that almost all roots are close to the critical line. Siegel has discovered these proofs in 1935 when he investigated Riemann’s estate. Riemann never published them. It was Hardy 1914 who first published a proof that there are infinitely many zeros on the critical line. A little later 1921, Hardy and Littlewood proved that there is a constant ##A>0## such that there are more than ##AT## zeros with real part ##1/2## whose (absolute) imaginary part is smaller than ##T.## It follows that there is a non-zero percentage ##B## of zeros on the critical line. Levinson showed in 1974 that ##B>1/3.##

It is not quite clear whether Hardy believed in God or was just superstitious. However, in any case, he believed God would do everything to make his life tough and complicated. One day, he was on a journey back home from a meeting with Harald Bohr (Niels Bohr’s brother) in Copenhagen. He had to take a ship and the boat he got didn’t look very trustworthy. Typically, he thought, why me? So he sent a postcard before boarding to Bohr claiming he had found the proof of Riemann’s hypothesis. When asked afterward, why, he replied: Well, if the ship sank the proof would have been lost but I would have become the most famous mathematician of my generation. God won’t allow this to happen. That way I only had to write Bohr another postcard in which I revealed to have made a mistake.

This anecdote and data demonstrate how famous the Riemann hypothesis was already at the beginning of the last century despite Riemann’s indifference to the problem that since carries his name.

Hilbert had been invited to give a lecture at the second International Congress of Mathematicians in August 1900 in Paris. He decided not to give a lecture in which he would report and appreciate what had been achieved in mathematics so far, nor to respond to Henri Poincaré’s lecture at the first International Congress of Mathematicians in 1897 on the relationship between mathematics and physics. Instead, his lecture was intended to offer a kind of programmatic outlook on future mathematics in the coming century. This objective is expressed in his introductory words:

“Who among us would not like to lift the veil that hides the future, to have a look at the forthcoming advances of our science and into the mysteries of its development during the centuries to come? What particular goals will it be that the leading mathematical minds of generations to come will aspire to? What new methods and new facts will the new centuries discover in the vast and rich field of mathematical thought?”

He, therefore, took the congress as an opportunity to compile a thematically diverse list of unsolved mathematical problems. As early as December 1899 he began to think about the subject. At the beginning of the new year, he then asked his close friends Hermann Minkowski and Adolf Hurwitz for suggestions as to which areas a corresponding lecture should cover; both read the manuscript and commented on it before the lecture. However, Hilbert only finally wrote down his list immediately before the congress – which is why it does not yet appear in the official congress program. The lecture was originally supposed to be given at the opening, but Hilbert was still working on it at the time. Now they are known as Hilbert’s 23 problems. There has been found a 24th in his estate: “How can the simplicity of a mathematical proof be measured, and how can its minimum be found?”, but the official count is 23. They are in part very specific like the first one: “Prove the continuum hypothesis.” even if not necessarily solvable, or very vague like the sixth one: “Mathematical treatment of the axioms of physics.” Here we are interested in the eighth: Prove the Riemann hypothesis, the Goldbach conjecture, and the twin prime conjecture. [3]

“Recently, significant advances have been made in the theory of the distribution of prime numbers by Hadamard, de La Vallee-Poussin, V. Mangoldt, and others. However, to completely solve the problems posed by Riemann’s treatise ‘On the Number of Primes Below a Given Size’, it is still necessary to prove the correctness of Riemann’s extremely important claim that the zeros of the function ##\zeta(s)##, which is defined by the series ##\zeta (s)=1+\frac{1}{2^{s}}+\frac{1}{3^{s}}+\cdots ##, all have the real components ##1/2## if one disregards the well-known negative integer zeros. As soon as this proof is successful, the further task would be to examine the Riemann infinite series for the number of primes more precisely and in particular to decide whether the difference between the number of primes below a magnitude and the integral logarithm of ##x## becomes no higher than the ##\tfrac{1}{2}##th order in ##x## at infinity, and further, whether those from the first complex zeros of the function ##\zeta (s)## dependent terms of Riemann’s formula cause the local compression of the prime numbers, which one noticed when counting the prime numbers.” [13]

Yes, language was a different one a century ago. Hilbert himself classified the Riemann hypothesis as less difficult than, for example, the Fermat problem: in a lecture in 1919 he expressed the hope that a proof would be found in his lifetime, in the case of the Fermat conjecture perhaps in the lifetime of the youngest listeners; he considered the transcendence proofs in his 7th problem to be the most difficult – a problem that was solved in the 1930s by Gelfond and Theodor Schneider. The Fermat problem was solved in 1995 by Andrew Wiles and Richard Taylor as part of their proof of the modularity theorem. A proof that is not only rather long but also rather technical and complicated, so the comparison with the Riemann hypothesis is possibly not as far-fetched as it may sound.

“If I were to awaken after having slept for a thousand years, my first question would be: Has the Riemann hypothesis been proven?” (David Hilbert) [6]

Let’s summarize the central limit theorem of probability theory by considering a fair coin toss and we pay +1 for heads and cash in -1 for tails. The famous gambler’s fallacy is to believe that after a long straight of heads, a tail would become more likely. This is wrong because randomness has no memory. Chances are still fifty-fifty. Even our overall gain or loss ##L(n)## after ##n## tosses isn’t zero. It is as unlikely that there will be the same number of heads as there are tails as it is that all tosses would be heads. However, it can be proven that the probability distribution of ##L(n)## converges pointwise to a normal distribution, in our case the standard normal distribution which is the statement of the central limit theorem.

We have already seen the connection between the Riemann hypothesis and randomness $$ \operatorname{RH}(\theta)\quad \Longleftrightarrow\quad a_{even}(n)-a_{odd}(n) = O\left(n^{\theta +\varepsilon }\right)\text{ for all }\varepsilon >0. $$ Let us consider the Liouville function ##\lambda (n)=(-1)^{\#\text{ prime factors of }n}## and remember that ##a_{even/odd}(n)## counted the number of integers below ##n## that are a product of an even/odd number of primes. Then $$ L(n)=\sum_{k=1}^n \lambda (k)= a_{even}-a_{odd} $$ and the central limit theorem says $$ \lim_{n \to \infty}\dfrac{L(n)}{n^{\varepsilon +1/2}}=0 \text{ for all }\varepsilon >0 \Leftrightarrow L(n)=O(n^{\varepsilon +1/2}) \Leftrightarrow RH(1/2)$$ This means that the pseudo-randomness of the distribution of prime numbers is almost independent and identical, i.e. truly random. It seems Euler was right once more.

Number Theory

We already mentioned the fascination with prime numbers and their central meaning in number theory. It is no coincidence that there are three famous problems listed under Hilbert’s 8th problem:

Riemann Hypothesis ##a_{even}(n)-a_{odd}(n)=O(n^{\varepsilon +1/2})##
Goldbach’s Conjecture Every even integer greater than ##2## is the sum of two primes.
Twin Prime Conjecture There are infinitely many pairs ##(p,p+2)## of prime numbers ##p.##

Neither of these conjectures are proven although they have been tested for incredibly large amounts of numbers computationally. They all have to do with prime numbers. An integer ##p## is prime, if and only if ## (p-1)!\equiv -1 {\pmod p}## ( Wilson’s theorem ), and a pair ##(p,p+2)## is a pair of primes, if and only if ##4\cdot ((p-1)!+1)+p \equiv 0 {\pmod {p\cdot (p+2)}}## ( Clement’s theorem ).

Goldbach’s conjecture or the strong Goldbach conjecture has a weaker version: Every odd number greater than ##5## is the sum of three primes. Since ##3## is prime and ##2n+1=2n-2+3=p+q+3,## the strong version implies the weaker, which has been partially solved. On one hand, is it true in case the extended Riemann hypothesis holds, and on the other hand, it holds for sufficiently large numbers? If ##R(n)## is the number of representations of ##n## as the sum of three prime numbers, then ( Vinogradov’s theorem ) $$ R(n)=\dfrac{n^2}{2(\log n)^3}\underbrace{\left(\prod_{p\mid n}\left(1-\dfrac{1}{(p-1)^2}\right)\right)\left(\prod_{p\nmid n}\left(1+\dfrac{1}{(p-1)^3}\right)\right)}_{=:G(n)}+O\left(\dfrac{n^2}{(\log n)^4}\right) $$ and it can be shown that ##G(2n)=0,## ##G(2n-1)\geq 1,## and ##G(2n-1)## is asymptotically of order ##O(1),## hence ##R(2n-1)>0## for sufficiently large ##n.##

There have been quite a few attempts to tackle the problem by physical methods, especially lately. This is quite surprising since mathematics is a deductive science and physics a descriptive science. One can check the results of theoretical models in the physical world, but how should real-world observations contribute to a mathematical conjecture? The origin of such a connection, however, isn’t quite new. David Hilbert and Pólya György had already noticed that the Riemann hypothesis would follow if the zeros were eigenvalues of an operator ##({\tfrac{1}{ 2}}+iT)## where ##T## is a Hermitian (i.e. self-adjoint) operator, which therefore has only real eigenvalues, similar to the Hamiltonian operators in quantum mechanics. Further considerations in this direction end up in the theory of quantum chaos. Other connections have been drawn to statistical mechanics [3], or one-dimensional quasi-crystals [15]. We even had a visitor on Physics Forums who attempted to access it via the hydrogen atom. All these thoughts are based on parallels between the Riemann hypothesis and probability distributions and are often due to similarities in formulas.

In addition to numerous applications in many areas of mathematics, the Riemann Hypothesis is also of interest in cryptology. For example, the RSA cryptosystem uses large prime numbers to construct both public and private keys. Its security is based on the fact that conventional computers do not yet have an efficient algorithm for dividing a number into its prime factors, i.e. to solve FP. The theory behind RSA requires only results from elementary number theory. In 1976, again based on simple number theory and using Fermat’s little theorem, Miller developed a deterministic primality test that works assuming the extended Riemann Hypothesis [16]. In 1980, Michael O. Rabin used Miller’s results to develop a probabilistic test that worked independently of the extended Riemann hypothesis [17]. Through the work of Bach in 1990, this so-called Miller-Rabin test can be converted into a deterministic test that runs with the speed ##O(\log(n)^{2})##, again assuming the extended Riemann Hypothesis [10]. All the connections between the Riemann hypothesis and cryptology are at their core due to their meaning for the distribution of prime numbers.

[1] A.K. Lenstra, Fast and rigorous factorization under the generalized Riemann hypothesis, Indagationes Mathematicae (Proceedings), Volume 91, Issue 4, 1988, Pages 443-454, ISSN 1385-7258

[2] German Wikipedia, Primzahlsatz https://commons.wikimedia.org/wiki/File:PrimeNumberTheorem.svg https://de.wikipedia.org/wiki/Riemannsche_Vermutung

[3] Wikipedia https://de.wikipedia.org/wiki/Riemannsche_Vermutung https://de.wikipedia.org/wiki/Goldbachsche_Vermutung https://de.wikipedia.org/wiki/Hilbertsche_Probleme https://en.wikipedia.org/wiki/Hilbert%27s_problems https://en.wikipedia.org/wiki/Twin_prime#Twin_prime_conjecture

[4] Otto Forster, München 2017/2018, 8. Äquivalenzen zur Riemannschen Vermutung https://www.mathematik.uni-muenchen.de/~forster/v/zrh/vorlzrh_chap8.pdf

[5] The Extended Riemann Hypothesis and Ramanujan’s Sum https://www.physicsforums.com/insights/the-extended-riemann-hypothesis-and-ramanujans-sum/

[6] AZ Quotes https://www.azquotes.com/author/6689-David_Hilbert

[7] Maier, Haase, Analytical Number Theory, Ulm 2007 (in German) https://www.uni-ulm.de/fileadmin/website_uni_ulm/mawi.inst.zawa/lehre/12sem-pz/Analytische_Zahlentheorie_SS_2007.pdf

[8] W. Dittrich, On Riemann’s Paper, “On the Number of Primes Less Than a Given Magnitude”, Tübingen 2017 https://arxiv.org/pdf/1609.02301.pdf

[9] Bernhard Riemann, On the Number of Prime Numbers less than a Given Quantity. (Über die Anzahl der Primzahlen unter einer gegebenen Grösse. [Monatsberichte der Berliner Akademie, November 1859.]) Translated by David R. Wilkins, 1998 https://www.claymath.org/sites/default/files/ezeta.pdf

[10] Eric Bach, Explicit Bounds for Primality Testing and Related Problems, Mathematics of Computation, Volume 55, Number 191, July 1990, pages 355-380 https://www.ams.org/journals/mcom/1990-55-191/S0025-5718-1990-1023756-8/S0025-5718-1990-1023756-8.pdf

[11] X. Gourdon, The 10E13 first zeros of the Riemann Zeta function, and zeros computation at very large height (2004) http://numbers.computation.free.fr/Constants/Miscellaneous/zetazeros1e13-1e24.pdf

[12] Jean Dieudonné, Geschichte der Mathematik 1700-1900, Vieweg Verlag 1985

[13] Julian Havil, Gamma. Springer-Verlag, Berlin et al. 2007, p. 244-245.

[14] H.M.Edwards, Riemann’s Zeta Function, Dover Publications Inc., 2003 (315 pages) https://www.amazon.de/Riemanns-Function-Dover-Mathematics-Applied/dp/0486417409/ref=asc_df_0486417409/

[15] Freman Dyson, Birds and Frogs, 2009 https://www.ams.org//notices/200902/rtx090200212p.pdf

[16] Gary L. Miller, Riemann’s Hypothesis and Tests for Primality, Journal of Computer and System Sciences, 1976, 13(3), p. 300–317.

[17] M. O. Rabin, Probabilistic algorithm for testing primality, Journal of Number Theory, 1980, 12(1), p. 128–138.

Riemann’s influence

Differential equations
Linear algebra
The foundations of geometry
The foundations of mathematics
Mathematical physics
Algebraic topology
Developments in pure mathematics
Mathematical physics and the theory of groups
Probabilistic mathematics

Our editors will review what you’ve submitted and determine whether to revise the article.

LiveScience - What is Mathematics?
Social Sci LibreTexts - Mathematics
PBS LearningMedia - Ancient Math & Music
Official Site of The Abel Prize
University of California, San Diego - What is Mathematics?
mathematics - Children's Encyclopedia (Ages 8-11)
mathematics - Student Encyclopedia (Ages 11 and up)
Table Of Contents

When Gauss died in 1855, his post at Göttingen was taken by Peter Gustav Lejeune Dirichlet . One mathematician who found the presence of Dirichlet a stimulus to research was Bernhard Riemann , and his few short contributions to mathematics were among the most influential of the century. Riemann’s first paper, his doctoral thesis (1851) on the theory of complex functions, provided the foundations for a geometric treatment of functions of a complex variable . His main result guaranteed the existence of a wide class of complex functions satisfying only modest general requirements and so made it clear that complex functions could be expected to occur widely in mathematics. More important, Riemann achieved this result by yoking together the theory of complex functions with the theory of harmonic functions and with potential theory . The theories of complex and harmonic functions were henceforth inseparable.

Recent News

Riemann then wrote on the theory of Fourier series and their integrability. His paper was directly in the tradition that ran from Cauchy and Fourier to Dirichlet, and it marked a considerable step forward in the precision with which the concept of integral can be defined. In 1854 he took up a subject that much interested Gauss, the hypotheses lying at the basis of geometry .

The study of geometry has always been one of the central concerns of mathematicians. It was the language, and the principal subject matter, of Greek mathematics, was the mainstay of elementary education in the subject, and has an obvious visual appeal. It seems easy to apply, for one can proceed from a base of naively intelligible concepts. In keeping with the general trends of the century, however, it was just the naive concepts that Riemann chose to refine. What he proposed as the basis of geometry was far more radical and fundamental than anything that had gone before.

Riemann took his inspiration from Gauss’s discovery that the curvature of a surface is intrinsic , and he argued that one should therefore ignore Euclidean space and treat each surface by itself. A geometric property, he argued, was one that was intrinsic to the surface. To do geometry, it was enough to be given a set of points and a way of measuring lengths along curves in the surface. For this, traditional ways of applying the calculus to the study of curves could be made to suffice . But Riemann did not stop with surfaces. He proposed that geometers study spaces of any dimension in this spirit—even, he said, spaces of infinite dimension.

Several profound consequences followed from this view. It dethroned Euclidean geometry , which now became just one of many geometries. It allowed the geometry of Bolyai and Lobachevsky to be recognized as the geometry of a surface of constant negative curvature, thus resolving doubts about the logical consistency of their work. It highlighted the importance of intrinsic concepts in geometry. It helped open the way to the study of spaces of many dimensions. Last but not least, Riemann’s work ensured that any investigation of the geometric nature of physical space would thereafter have to be partly empirical . One could no longer say that physical space is Euclidean because there is no geometry but Euclid’s . This realization finally destroyed any hope that questions about the world could be answered by a priori reasoning.

In 1857 Riemann published several papers applying his very general methods for the study of complex functions to various parts of mathematics. One of these papers solved the outstanding problem of extending the theory of elliptic functions to the integration of any algebraic function . It opened up the theory of complex functions of several variables and showed how Riemann’s novel topological ideas were essential in the study of complex functions. (In subsequent lectures Riemann showed how the special case of the theory of elliptic functions could be regarded as the study of complex functions on a torus .)

In another paper Riemann dealt with the question of how many prime numbers are less than any given number x . The answer is a function of x , and Gauss had conjectured on the basis of extensive numerical evidence that this function was approximately x /ln( x ). This turned out to be true, but it was not proved until 1896, when both Charles-Jean de la Vallée Poussin of Belgium and Jacques-Salomon Hadamard of France independently proved it. It is remarkable that a question about integers led to a discussion of functions of a complex variable, but similar connections had previously been made by Dirichlet. Riemann took the expression Π(1 − p − s ) −1 = Σ n − s , introduced by Euler the century before, where the infinite product is taken over all prime numbers p and the sum over all whole numbers n , and treated it as a function of s . The infinite sum makes sense whenever s is real and greater than 1. Riemann proceeded to study this function when s is complex (now called the Riemann zeta function ), and he thereby not only helped clarify the question of the distribution of primes but also was led to several other remarks that later mathematicians were to find of exceptional interest. One remark has continued to elude proof and remains one of the greatest conjectures in mathematics: the claim that the nonreal zeros of the zeta function are complex numbers whose real part is always equal to 1/2.

In 1859 Dirichlet died and Riemann became a full professor, but he was already ill with tuberculosis, and in 1862 his health broke. He died in 1866. His work, however, exercised a growing influence on his successors. His work on trigonometric series , for example, led to a deepening investigation of the question of when a function is integrable. Attention was concentrated on the nature of the sets of points at which functions and their integrals (when these existed) had unexpected properties. The conclusions that emerged were at first obscure, but it became clear that some properties of point sets were important in the theory of integration, while others were not. (These other properties proved to be a vital part of the emerging subject of topology .) The properties of point sets that matter in integration have to do with the size of the set. If one can change the values of a function on a set of points without changing its integral , it is said that the set is of negligible size. The naive idea is that integrating is a generalization of counting: negligible sets do not need to be counted. About the turn of the century the French mathematician Henri-Léon Lebesgue managed to systematize this naive idea into a new theory about the size of sets, which included integration as a special case. In this theory, called measure theory , there are sets that can be measured, and they either have positive measure or are negligible (they have zero measure), and there are sets that cannot be measured at all.

The first success for Lebesgue’s theory was that, unlike the Cauchy-Riemann integral, it obeyed the rule that if a sequence of functions f n ( x ) tends suitably to a function f ( x ), then the sequence of integrals ∫ f n ( x ) d x tends to the integral ∫ f ( x ) d x . This has made it the natural theory of the integral when dealing with questions about trigonometric series. ( See the figure.) Another advantage is that it is very general. For example, in probability theory it is desirable to estimate the likelihood of certain outcomes of an experiment. By imposing a measure on the space of all possible outcomes, the Russian mathematician Andrey Kolmogorov was the first to put probability theory on a rigorous mathematical footing.

Another example is provided by a remarkable result discovered by the 20th-century American mathematician Norbert Wiener : within the set of all continuous functions on an interval, the set of differentiable functions has measure zero. In probabilistic terms, therefore, the chance that a function taken at random is differentiable has probability zero. In physical terms, this means that, for example, a particle moving under Brownian motion almost certainly is moving on a nondifferentiable path. This discovery clarified Albert Einstein’s fundamental ideas about Brownian motion (displayed by the continual motion of specks of dust in a fluid under the constant bombardment of surrounding molecules). The hope of physicists is that Richard Feynman’s theory of quantum electrodynamics will yield to a similar measure-theoretic treatment, for it has the disturbing aspect of a theory that has not been made rigorous mathematically but accords excellently with observation.

Yet another setting for Lebesgue’s ideas was to be the theory of Lie groups . The Hungarian mathematician Alfréd Haar showed how to define the concept of measure so that functions defined on Lie groups could be integrated . This became a crucial part of Hermann Weyl ’s way of representing a Lie group as acting linearly on the space of all (suitable) functions on the group (for technical reasons, suitable means that the square of the function is integrable with respect to a Haar measure on the group).

from the web

The Riemann hypothesis, a Step Closer to Being Solved

09/07/2024 10/07/2024
from the web , web archive

The Biggest Problem in Mathematics Is Finally a Step Closer to Being Solved Scientific American Nineteenth-century German mathematician Bernhard Riemann proposed a way to deal with this peculiarity that explains how prime numbers are distributed … link

Other experts agree. The work is “a remarkable breakthrough,” mathematician and Fields Medalist Terence Tao wrote on Mastodon , “though still very far from fully resolving this conjecture.”

The Riemann hypothesis concerns the basic building blocks of natural numbers: prime numbers, values only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, 13, and so on.

There are now numerous theorems based on the Riemann conjecture. Proof of this conjecture would prove many other theorems as well—yet another incentive to tackle this stubborn problem.

Interest in prime numbers goes back thousands of years. Euclid proved as early as 300 BCE that there are an infinite number of prime numbers. And although interest in prime numbers persisted, it was not until the 18th century that any further significant findings were made about these basic building blocks.

… Here are 8 notable Indian mathematicians who changed the world! Business Insider India By: Ankush Banerjee. Credit: iStock. A haven for mathematicians. India has a rich history of mathematical innovation, with many mathematicians … link

Amateur Mathematicians Find Fifth ‘Busy Beaver’ Turing Machine – Quanta Magazine Quanta Magazine Beavers enter the story with the mathematician Tibor Radó, who was no stranger to long journeys. Born in Hungary in 1895, he entered university to … link

The climate mathematician – Scienceline Scienceline The climate mathematician. As the world warms, scientist David Holland is building a weather forecast for the polar ice caps. Gayoung Lee • June 25 … link

New book by mathematicians David Angell and Thomas Britz – UNSW Sydney UNSW Sydney New book by mathematicians David Angell and Thomas Britz. The book launch coincides with the 60th anniversary of the School’s maths journal … link

Mathematician Hannah Fry: ‘Even though Labour will win, they should dampen their expectations’ The Telegraph Most brilliant mathematicians stick to the lecture circuit. Fry, 40 who is a professor in the mathematics of cities at UCL, hosts the AI podcast … link

India is a powerhouse of mathematics, says Krishnaswami Alladi – The Hindu The Hindu The autobiography of reputed mathematician Krishnaswami Alladi titled My Mathematical Universe-People, Personalities and The Profession was … link

Black Heroes in Mathematics – Wilson’s School Wilson’s School We were very fortunate to be joined by Professor Nira Chamberlain OBE. Dr Chamberlain, a Chartered Scientist, Chartered Mathematician, … link

Vegetarians used to be called Pythagoreans because the famous mathematician loathed by … – MSN Vegetarians used to be called Pythagoreans because the famous mathematician loathed by high … Vegetarians used to be called Pythagoreans because the famous mathematician loathed by high schoolers everywhere refused to eat meat. Story by … link

Young mathematician hopes to showcase talent at international competition – IOL IOL Suhrit Avaneesh Pitchaimuthu Sridhar has been selected to represent South Africa at the India International Mathematics Competition (InIMC) in … link

$riemann hypothesis$

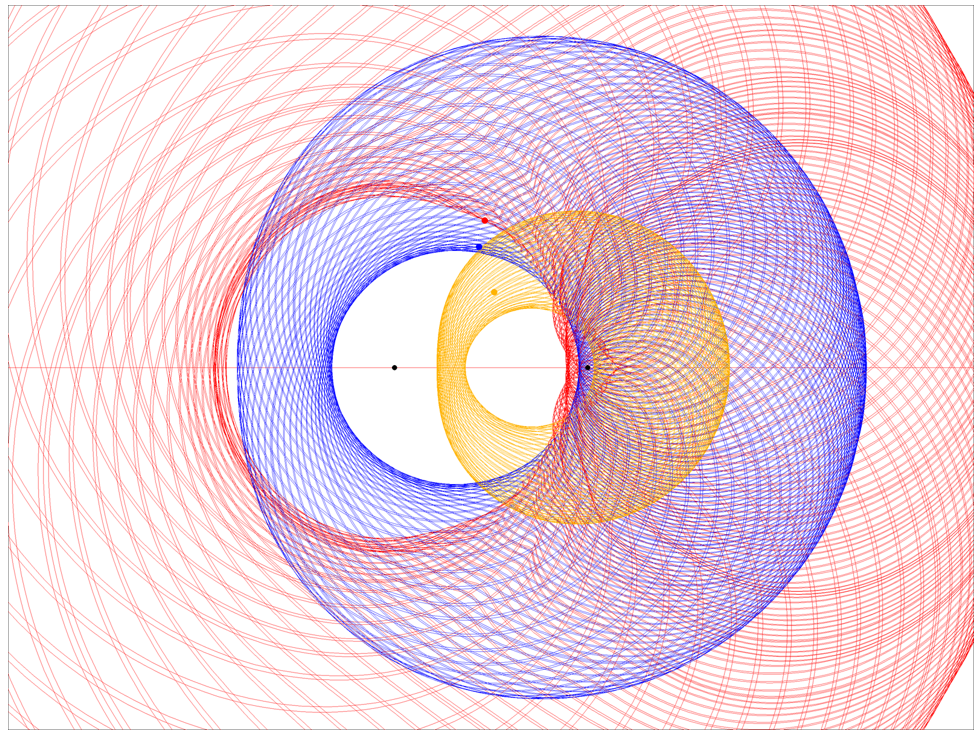
Artificial Intelligence in Education: More Questions Than Answers
Flex-Based Schools: A Revolution in Education?
The one-off aid for students in Bulgaria
How Does Math Keep Secrets?
Olympic Swimmers Think About Math in the Pool
Bulgarian education abroad…
How history could inspire the future of education
Fewer and fewer students are taking the Grade 12 maths exam
20 schools in Sofia will have new principals
A.I. Can Write Poetry, but It Struggles With Math

Search Clay Mathematics Institute

Home — Lectures — Riemann hypothesis

Riemann hypothesis

In 2001, the University of Texas, Austin held a series of seven general audience evening lectures, “The Millennium Lectures”, based on the “Millennium Prize Problems.” Their aim was to explain to a wide audience the historical background to these problems, why they have resisted many years of serious attempts to solve them, and the roles these problems play in modern mathematics. The lecture series ran throughout the Spring Semester 2001 and were given by members of Departments of Mathematics and Computer Science.

Research & Academics
Clicking the menu button will open up an expanded version of the navigation. Menu
Research and Academics
Diversity, Equity, and Inclusion

Academic Departments

Helpful resources, support science.

Please contact Elizabeth Chadis if you are considering a gift to the School of Science.

The Riemann Hypothesis, the Biggest Problem in Mathematics, Is a Step Closer to Being Solved

Read it at Scientific American

Brain and Cognitive Sciences
Earth, Atmospheric and Planetary Sciences
Mathematics
Massachusetts Institute of Technology
Accessibility
For Emergencies
Community Conduct

IMAGES

A Direct Proof of the Riemann Hypothesis
A Direct Proof of the Riemann Hypothesis
What is the Riemann Hypothesis in Simple Terms? » Mathematics
The Riemann Hypothesis: What Is It, Exactly?
Suppose that Riemann Hypothesis is Correct
kmyc89's modify the Riemann hypothesis formula

COMMENTS

Riemann hypothesis
The Riemann hypothesis implies that the zeros of the zeta function form a quasicrystal, a distribution with discrete support whose Fourier transform also has discrete support. Dyson (2009) suggested trying to prove the Riemann hypothesis by classifying, or at least studying, 1-dimensional quasicrystals.
Riemann Hypothesis -- from Wolfram MathWorld
First published in Riemann's groundbreaking 1859 paper (Riemann 1859), the Riemann hypothesis is a deep mathematical conjecture which states that the nontrivial Riemann zeta function zeros, i.e., the values of s other than -2, -4, -6, ... such that zeta(s)=0 (where zeta(s) is the Riemann zeta function) all lie on the "critical line" sigma=R[s]=1/2 (where R[s] denotes the real part of s). A ...
Riemann hypothesis
A proof of the Riemann hypothesis would have far-reaching consequences for number theory and for the use of primes in cryptography.. The Riemann hypothesis has long been considered the greatest unsolved problem in mathematics.It was one of 10 unsolved mathematical problems (23 in the printed address) presented as a challenge for 20th-century mathematicians by German mathematician David Hilbert ...
Here's why we care about attempts to prove the Riemann hypothesis
The Riemann hypothesis is a conjecture about the Riemann zeta function, which is related to prime numbers. It has never been proved, but a recent attempt by a renowned mathematician has sparked interest and skepticism.
The Riemann Hypothesis, the Biggest Problem in Mathematics, Is a Step
The Riemann hypothesis concerns the basic building blocks of natural numbers: prime numbers, values greater than 1 that are only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, 13 ...
Riemann Hypothesis
Learn about the Riemann hypothesis, a famous unsolved problem in number theory that relates the distribution of prime numbers to the zeta function. Find out why it is important, how it is formulated, and what progress has been made.
2.5: The Riemann Hypothesis
Conjecture 2.22 (Riemann Hypothesis) All non-real zeros of ζ(s) ζ ( s) lie on the line Res = 12 Re s = 1 2. In his only paper on number theory [ 20 ], Riemann realized that the hypothesis enabled him to describe detailed properties of the distribution of primes in terms of of the location of the non-real zero of \ (\zeta ( s )\).
PDF The Riemann Hypothesis
A survey of the history, status, and approaches to the Riemann Hypothesis, a famous conjecture about the zeros of the Riemann zeta-function. The article covers topics such as the functional equation, the prime number theorem, the convexity bound, and the recent workshops on RH.
Has one of math's greatest mysteries, the Riemann hypothesis, finally
Sir Michael Atiyah, a renowned mathematician, claims to have solved the Riemann hypothesis, one of the Clay Mathematics Institute's Million Dollar Problems. The Riemann hypothesis concerns the distribution of prime numbers and the location of the zeros of the Riemann zeta function.
Riemann Hypothesis
The Riemann Hypothesis is a famous conjecture in analytic number theory that states that all nontrivial zeros of the Riemann zeta function have real part.From the functional equation for the zeta function, it is easy to see that when .These are called the trivial zeros. This hypothesis is one of the seven millenium questions.. The Riemann Hypothesis is an important problem in the study of ...
PDF THE RIEMANN HYPOTHESIS
A proof of the Riemann hypothesis is claimed for the Euler zeta function based on a generalization of the gamma function and a Radon transformation. The proof uses quaternions, hyperbolic analysis, Hecke operators, and Fourier analysis on locally compact Abelian groups.
PDF Riemann'S Hypothesis
1. ( 1)nbntn : (2n)! n=0is entire of order 1/2 and the Riemann Hypothesis implies that all of its zeros are real, and in addition, that all of the zeros of all derivat. ves Y (m)(t) are real. From the Grommer inequalities, a necessary condition for all of the zeros of Y (t) to be re.
A Primer on the Riemann Hypothesis
An introduction for physicists into the Riemann Hypothesis, a conjecture about the zeros of the Riemann zeta function and the distribution of primes. The article compares and contrasts the Riemann function and the Dirichlet L-functions, and connects them to quantum mechanics and random matrices.
The Riemann Hypothesis, Explained
The Riemann Hypothesis is the most notorious unsolved problem in all of mathematics. Ever since it was first proposed by Bernhard Riemann in 1859, the conjec...
Mathematicians report possible progress on the Riemann hypothesis
A new study of Jensen polynomials revives an old approach to the Riemann hypothesis, a statement about the Riemann zeta function and prime numbers. The researchers show that many of these polynomials have real roots, but the proof is still elusive.
The History and Importance of the Riemann Hypothesis
The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field of number theory. It's named after the German mathematician Bernhard Riemann, who introduced the hypothesis in 1859. RH: All non-trivial zeros of the Riemannian zeta function lie on the critical line.
Mathematics
Mathematics - Riemann Hypothesis, Complex Analysis, Number Theory: When Gauss died in 1855, his post at Göttingen was taken by Peter Gustav Lejeune Dirichlet. One mathematician who found the presence of Dirichlet a stimulus to research was Bernhard Riemann, and his few short contributions to mathematics were among the most influential of the century.
The Riemann hypothesis, a Step Closer to Being Solved
The Riemann hypothesis is the most important open question in number theory—if not all of mathematics. It has occupied experts for more than 160 years. And the problem appeared both in mathematician David Hilbert's groundbreaking speech from 1900 and among the "Millennium Problems" formulated a century later. The person who solves it ...
Riemann hypothesis
Learn what the Riemann hypothesis is, why it is important, and how it is related to prime numbers and complex numbers. See a picture of the Riemann zeta function and its non-trivial roots, and find out what we know and don't know about them.
Riemann Hypothesis
The Riemann Hypothesis.More links & stuff in full description below ... Featuring Professor Edward Frenkel. Here is the biggest (?) unsolved problem in maths... The Riemann Hypothesis.More links ...
Riemann hypothesis
Riemann hypothesis. In 2001, the University of Texas, Austin held a series of seven general audience evening lectures, "The Millennium Lectures", based on the "Millennium Prize Problems." Their aim was to explain to a wide audience the historical background to these problems, why they have resisted many years of serious attempts to ...
The Riemann Hypothesis, the Biggest Problem in Mathematics, Is a Step
The Riemann Hypothesis, the Biggest Problem in Mathematics, Is a Step Closer to Being Solved. Read it at Scientific American. Published July 01, 2024 Tagged Larry Guth Mathematics. MIT School of Science. Biology; Brain and Cognitive Sciences; Chemistry; Earth, Atmospheric and Planetary Sciences;

Riemann Hypothesis

Explore with Wolfram|Alpha

Cite this as:

Subject classifications

The Biggest Problem in Mathematics Is Finally a Step Closer to Being Solved

On supporting science journalism

A Periodic Table for Numbers

A Strange Connection

On the Hunt for Zeros

Has one of math’s greatest mysteries, the Riemann hypothesis, finally been solved?

Disclosure statement

Manager, Regional Training Hub

Head of Evidence to Action

Supply Chain - Assistant/Associate Professor (Tenure-Track)

OzGrav Postdoctoral Research Fellow

Casual Facilitator: GERRIC Student Programs - Arts, Design and Architecture

Riemann Hypothesis

A Primer on the Riemann Hypothesis

Cite this chapter

Access this chapter

Acknowledgements

Author information

Corresponding author

Editor information

Appendix 1: Functional Equation of Jacobi Theta Function

Appendix 2: Equivalent Condition for Non-trivial Zeros

Appendix 3: Exponential Product

1.1 General Expression

1.2 Asymptotic Limit

1.3 Special Case: Riemann Function

Appendix 4: Lines of Constant Height and Constant Phase

1.1 Decomposition in Amplitude and Phase

1.2 Special Limits

1.2.1 At the Center of the Complex Plane

1.2.2 At the Right Edge of the Complex Plane

1.3 Cauchy-Riemann Differential Equations

Appendix 5: Special Examples of Normalized Gauss Sums

1.1 Non-vanishing Phase

1.2 Vanishing Phase

Appendix 6: Functional Equation of Generalized Jacobi Theta Function

1.1 Extension of Summation

1.2 Emergence of Gauss Sum

1.3 Comparison to Jacobi Theta Function of \(\xi \)

Rights and permissions

Copyright information

About this chapter

Download citation

Share this chapter

Science News

Share this:

More Stories from Science News on Math

This intricate maze connects the dots on quasicrystal surfaces

Scientists find a naturally occurring molecule that forms a fractal

How two outsiders tackled the mystery of arithmetic progressions

Here’s how much fruit you can take from a display before it collapses

Here are some astounding scientific firsts of 2023

‘Is Math Real?’ asks simple questions to explore math’s deepest truths

An enduring Möbius strip mystery has finally been solved

The History and Importance of the Riemann Hypothesis

Riemann Hypothesis History

Prime Numbers

Early Glory

Number Theory

You might also like

Leave a Reply

Riemann’s influence

Recent News

The Riemann hypothesis, a Step Closer to Being Solved

Search Clay Mathematics Institute

Riemann hypothesis

Academic Departments

The Riemann Hypothesis, the Biggest Problem in Mathematics, Is a Step Closer to Being Solved

IMAGES

COMMENTS